A measure of spread, sometimes also called a measure of dispersion, is used to describe the variability in a sample or population.

Just like the measure of central tendency , we also have measures of the spread, which comprises of the following measures:

• Range: It is the given measure of how spread apart the values in a data set are. The range can be calculated as -

        Range = Max(x_i) - Min(x_i)
  
        Here,
  
        Max(x_𝑖): Maximum value of x
  
        Min(x_𝑖):  Minimum value of x
  

• Quartile: Quartiles tell us about the spread of a data set by breaking the data set into quarters.To better understand how quartile and the IQR are calculated, let’s look at an example.

  Consider a list containing Marks of students in a class-

        Marks=[10,11,12,15,17,18,19,20,22,23,24,25]
  

The quartiles lie in the following ranges:

• The first quartile (Q1) lies between the 3rd and 4th observation.

• The second quartile (Q2) lies between the 6th and 7th observation.

• The third quartile (Q3) lies between the 9th and 10th observation.

• Inter Quartile Range (IQR): It is the measure of variability, based on dividing a data set into quartiles. The interquartile range can be calculated as

        IQR = Q3 – Q1
  

Variance: It describes how much a random variable differs from its expected value.Variance can be calculated by using the below formula:

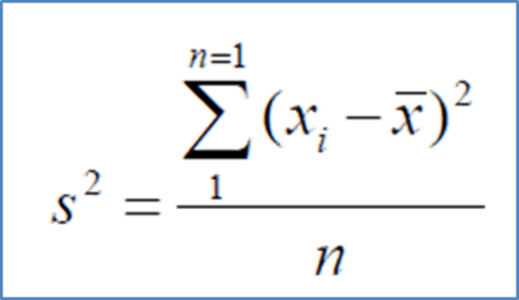
Here,

x: Individual data points n: Total number of data points x̅: Mean of data points

Deviation is the difference between each element from the mean. It can be calculated by using the below formula:

Deviation = (𝑥_𝑖 – µ)

• Population Variance is the average of squared deviations. It can be calculated by using the below formula:

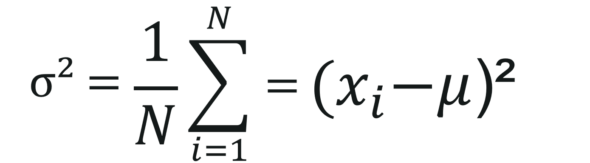
• Sample Variance is the average of squared differences from the mean. It can be calculated by using the below formula:

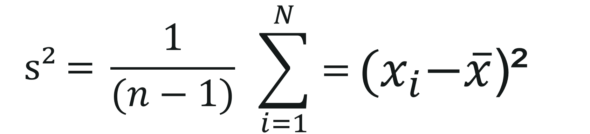
• Standard Deviation: It is the measure of the dispersion of a set of data from its mean. It can be calculated by using the below formula:

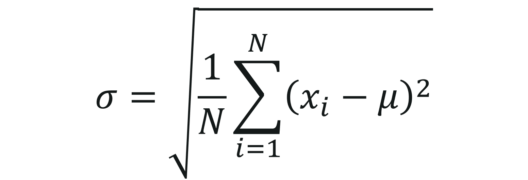
To better understand how the Measures of spread are calculated, will look at a use case in the upcoming blogs.

Thanks for Reading!! Happy Learning!!